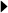「建築におけるセクション(断面図)の役割は死んだ」──米国、ペンシルヴァニア大学で教鞭をとる構造家セシル・バルモンドの言葉である。同大学建築学部は、二〇〇二年にミース研究で著名であるデトレフ・マーティンを学長に迎えて以来、その教育方針が大幅に変わることとなった。それまで同大の歴史を形づくってきたルイス・カーン時代の教授の大半が去り、代わりにアメリカやヨーロッパの若い建築家が多数集められることとなる。セシル・バルモンドを教授として迎え入れた翌年の二〇〇五年には非線形システム機構(NLSO)が創設され、同校の教育改革はより一層加速することとなる。
同大学の建築教育において、ライノ、マヤ、GC(Generative Components)をはじめとするソフトウェアを設計過程のごく初期の段階から使用することは基本となっている。複雑な幾何学の生成過程と、その過程上に存在するルールとシステムの分析と解明はコンピュータを使うことによって速く正確に導き出される。冒頭で述べたバルモンドの言葉は「断面図が不用である」という意味ではけっしてなく、設計過程においてのコンピュータの役割と、それが可能にする新しい設計アプローチへの期待も含まれているのである。
「CanArchitecture Heal?」と題されたバルモンド・スタジオの目的は、治療を目的とした医療施設、あるいはリラクゼーションを提供するスパのようなビルディングタイプを、物理的条件のスタディや行動人類学的見地からデザインするものとは、その設計に至る思考過程において一線を画するものである。学生たちには、自然界や生物学における幾何学的パターン、あるいは数学的アルゴリズムによって導き出されたシステムを分析し、さらに類型化された複数のモデル(以下1──10を参照)を探求し、それらを新しい建築タイプとして解釈することが求められている。それによって、従来の固定された制度から脱却し、より柔軟で応用的な回答を得、現在の医療におけるタイポロジーの再構成の可能性を探るということが最終的な目標課題とされている。
[福西健太]
Composite image of student work at PennDesign in the Research Studio of Cecil Balmond with Nick Desbians Spring 2005. Image generated by Jenny Sabin and Raymond Kettner. Students: Brandon Buck,
Nia Garner, Raymond Kettner, Chia Hua Liu, Josh Mackley, Andrew Mikhael, Matt Nowaczyk, Jenny Sabin, Tanya Samarasingha, and Joel Wenzel (Courtesy University of Pennsylvania).
1 Transform Data
ハーモニック・データを関数変換することによって、色、光、音や3次元メッシュ・モデルとして視覚化することが可能になる。フーリエ変換と呼ばれるこの手法を用い、医療画像や音楽など、多岐にわたる分野を分析する。
[以下、ジェニー・サビン]
2 Atom Growth
曲面を円で敷き詰めていくサークル・パッキングは自然界に見られる法則であるが、純粋幾何学においてそのパラメータは円の半径、重複や接触の度合に置き換えられる。付随的な諸条件や帰納的手法を用いることにより、単純な部分から形成される複雑な全体像を構成することを可能とする。
3 Branching Network
枝分かれ構造はその性質として、分節の長さ、分岐と重複の法則や性格といった単純な要素によって形態を決定する。それらのルール設定の操作により得られる多様な結果を通し、それぞれの結節点の関係性が枝分かれ構造におけるミクロとマクロの類似性を提示していることが明らかになる。
4 Circle Growth
ここでは、純粋な幾何学において発見されるサークル・パッキングの法則を故意に破壊していく。円同士の接点が失われると、サークルの成長を促すパラメータが支配する重複の度合が強まり、結果として螺旋形状を伴う重複部分が出現する。それぞれの円の中心点が連結されると、拡張した循環ネットワークがみてとれる。
5 Infectious Spread
このプロジェクトにおいて、ウイルスの分散と蔓延は一定の境界線内でコントロールされ制御される。免疫レヴェルと新種発生の確率がそれぞれのウイルスの拡大範囲を統制する。これらの関係性をネットワーク化したシステムが、都市における医療施設のマッピングの提案について新しい判断基準をもたらす。
6 L Systems
このプロジェクトにおいて、Lシステムとは多様な長さを持つ分節と分岐の成長過程のネットワーク構造を表現する手段である。単純なルール設定操作がその形態を変化させるため、それらのパターンを通してネットワークへのより詳細な理解が促される。
7 Woven Hybrid
“織り”とは2つの脆弱なシステムが構造的強度を伴うひとつの強固なシステムをつくりあげることと定義づけられる。つまりこの2層構造は2本の糸が双方の上へ下へと交互に織り込まれることによって形づくられている。この二重の情報の均整が取れたときに、織り目は強度を増す。このプロジェクトにおいては、2層のデータはジャガード折りと呼ばれるデジタル化された機械織りと接続され、黒と白の毛糸で編まれる。
8 Woven Data
人間の脈に基づいたハーモニック・データなど、生体システムから派生した一般データは点の集団に変換され、それぞれの点を曲線でつなぐことが可能となる。それら曲線に沿った各点の延長は、もとの生体データを3次元メッシュ・システムに置き換えることを可能にし、情報を新たなる方法において可視化する。
9 Data Revolution
波状システムは振幅と頻度といった単純なパラメータによって稼動される。ハーモニック・データはその延長として、ひとつの波、もしくは連続する複数の波として捉えらることもでき、またひとつの円から派生する曲線の循環としてみることもできる。複数の波状システムがひとつに重なったとき、複雑で美しいパターンが生まれる。それらは情報の多様な形態化の結果として使用される。
10 Color Data
人間の脈のような生体データを、さまざまな素材やデジタル・フォーマットに変換させることにより、個人や患者にとって新しい情報の可視化の方法を提案する。波状システムが深度と範囲を伴ったカラー・フィールドで示されている。